Ein Bezugssystem ist notwendig, wenn man z.B. eine Bewegung eines Körpers beschreiben möchte, oder wenn der Aufenthaltsort des Körpers angegeben werden muss. Da die Bewegung eines Körpers die Veränderung des Aufenthaltsortes ist, reichen tatsächlich die Daten, wann ein Körper wo ist.
Ein bekanntes Bezugssystem stellt das Gradnetz der Erdkugel dar. Mit dem Äquator bzw. den Breitengraden und dem Nullmeridian bzw. den Längengraden gibt es zwei Koordinaten, mit denen jeder Punkt auf der Erdoberflächen angesprochen werden kann. Mit der Meeresoberfläche und den Höhenlinien gibt es dann auch noch eine dritte Dimension, nämlich die Höhe.
Die Stadt Braunschweig z.B. findet man bei den Koordinaten 52,27 ° nördlicher Breite und 10,53 ° östlicher Länge sowie einer mittleren Höhe
über Normalnull von 70 m.
Ein ähnliches Prinzip wird für die Beschreibung von Bewegungen genutzt. Ein (willkürlich) gesetzter Ausgangspunkt (im Gradnetz der Erde ist das der Kreuzungspunkt zwischen Äquator und Nullmeridian) als Nullpunkt / Ursprung und zwei Richtungen (äquivalent zur Erdoberfläche) bzw. drei Richtungen (Erdoberfläche plus Höhe) dienen als Bezugssystem, um die Aufenthaltsorte eines Körpers zu verschiedenen Zeiten angeben zu können.
Da die Berechnungsgrundlage für die Beschreibung von Bewegungen die Mathematik ist, wird dieses Bezugssystem ein Koordinatensystem sein, bei dem die Richtungen mit x, y und z bezeichnet werden. Die Besonderheit bei dem Koordinatensystem ist nun, dass die Richtungen jeweils senkrecht zueinander stehen, was bei der Gradnetzeinteilung der Erdkugel nur auf der Kugel selbst gilt, nicht aber, wenn die Erdoberfläche auf eine zweidimensionale Ebene (z.B. ein Blatt Papier) abgebildet wird.
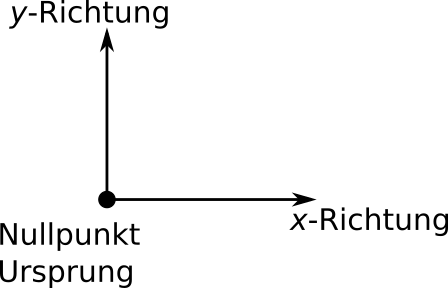Die Festlegung des Koordinatenursprungs bleibt willkürlich und wird im Allgemeinen von dem Sachzusammenhang abhängig gemacht. Üblicherweise
wird der Ursprung dorthin gelegt, wo die Beobachtung der Bewegung beginnt. Die Koordinaten (in zwei Dimensionen) wären dann: $x_0 = 0$ und
$y_0 = 0$, wobei auch festgelegt wird, dass die Koordinaten für den Beginn jeweils den Index Null erhalten. Die Festlegung der $x$- und der
$y$-Richtung ist wiederum abhängig vom Sachzusammenhang, ist aber prinzipiell beliebig.
Wenn wir in der Physik von Kräften auf Körper oder von Körpern in Bewegung sprechen, ist meistens von Körpern die Rede, die wir uns idealisiert als Massepunkte vorstellen sollen. Warum ist das so?
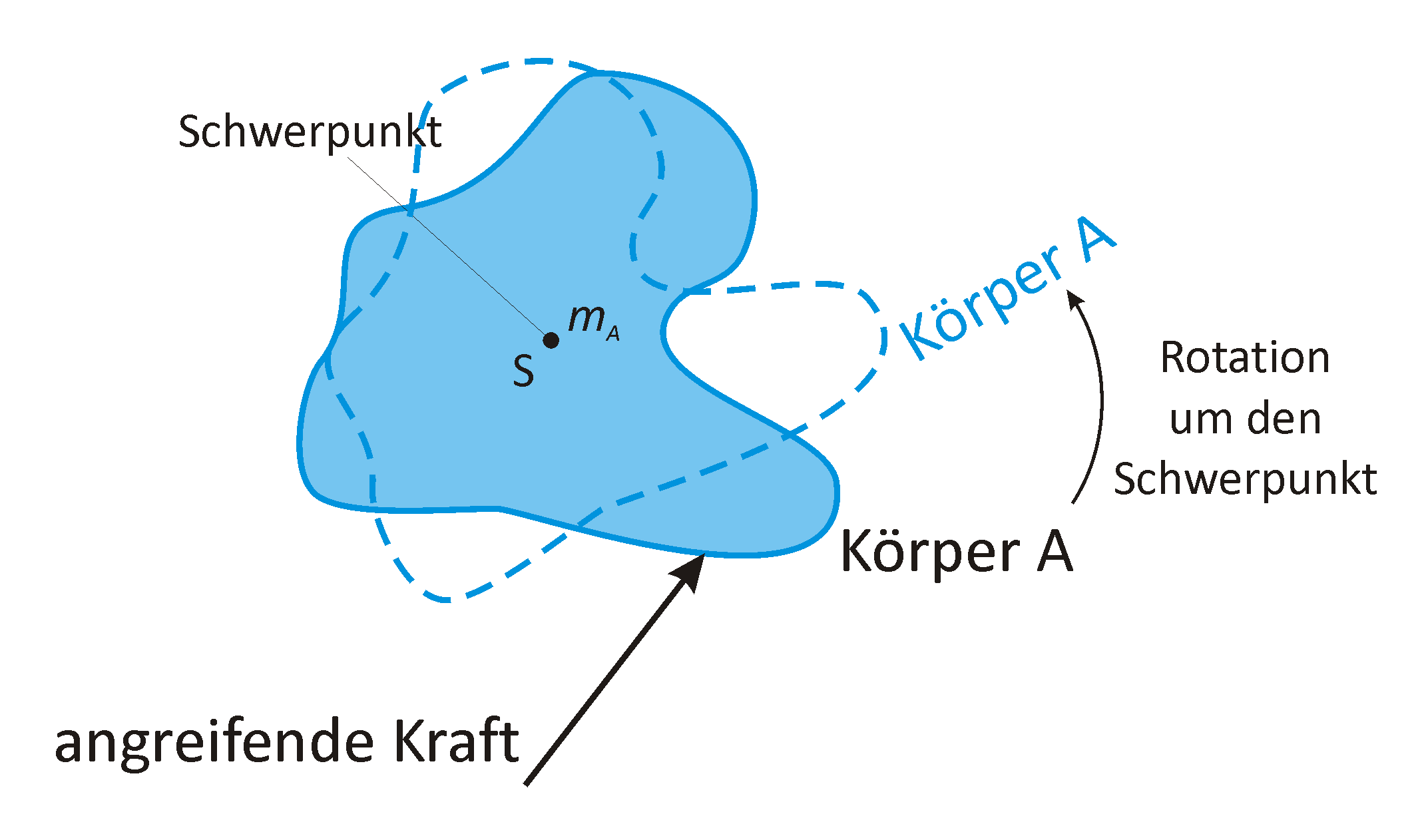Ausgedehnte Körper haben „irgendwo“ in ihrer Mitte ihren Schwerpunkt. Wenn nun an diesem
Körper eine Kraft angreift, dann tut sie das z.B. an einer der Körperecken, höchstwahrscheinlich
aber an einer Stelle, die etwas entfernt von dem Schwerpunkt liegt. Das würde dazu führen, dass der
Körper einen Teil seiner Bewegung, die er aufgrund der Kraft durchführt, in eine Rotation um seinen
Schwerpunkt wandeln würde. Diese Rotationsenergien und Drehimpulse sollen für den Anfang keine Rolle spielen.
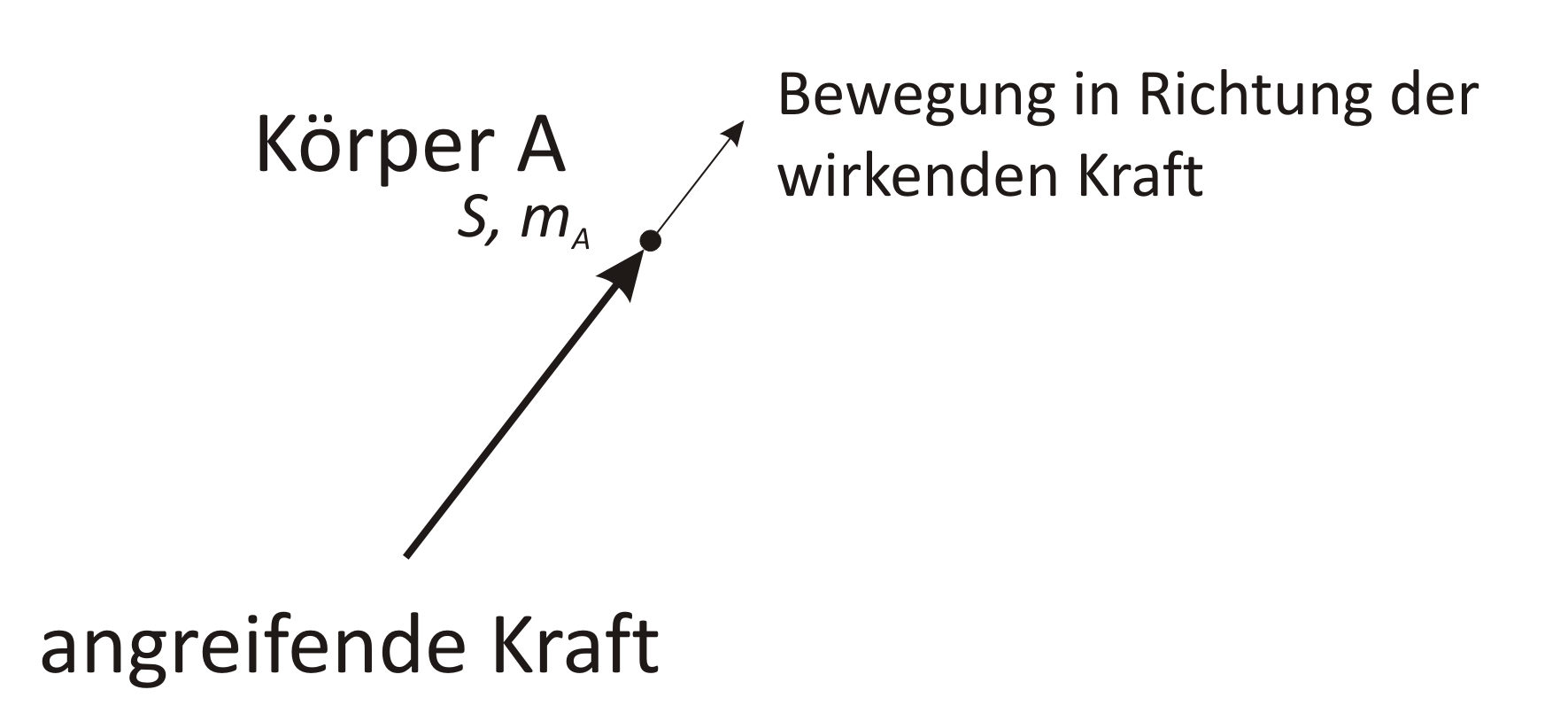Also denken wir uns die gesamte Masse des Körpers in einem Punkt zusammengefasst vor. An diesem Punkt greifen
alle Kräfte an, und alle Bewegungen werden von diesem Punkt durchgeführt. Wir müssen uns jetzt gar nicht
mehr um den eigentlichen Körper kümmern, denn der ist für die physikalische Untersuchung nicht wichtig.
Wie wir schon an den Abbildungen oben sehen können, haben z.B. Kräfte nicht nur eine Größe oder einen Betrag, sondern auch eine Richtung, nämlich die Richtung der Wirkung der Kraft. Aus dieser Kraftwirkung entsteht im Anschluss eine Bewegung in genau dieselbe Richtung. Kräfte sind gerichtete, vektorielle Größen, ebenso die aus der Kraft entstehenden Bewegungsgrößen Beschleunigung und Geschwindigkeit oder der Impuls.
| skalare Größen | vektorielle Größen |
|---|---|
|
|
Größen wie z.B. die Masse eines Körpers sind nicht abhängig von der Richtung. Sie sind überall und in allen Richtungen gleich. Diese Größen nennt man skalare Größen. Andere Beispiele, neben der Masse, sind z.B. die Temperatur oder die Energie.
Die skalaren Größen beschreiben den Zustand eines Objekts oder eines Systems. Dagegen beschreiben die vektoriellen Größen, wie sich der Zustand eines Objekts oder eines Systems in einen anderen Zustand ändert.
In den Abbildungen oben ist die wirkende Kraft als Pfeil dargestellt. Die Richtung der Größe entspricht der Richtung des Pfeils. Der Betrag der Größe wird von der Länge des Pfeils symbolisiert. Das bedeutet, je länger der Pfeil, desto größer der Betrag.
Gerichtete Größen nennt man auch Vektoren. Sie werden mit einem Pfeil über dem Formelzeichen dargestellt, z.B. für die gerichtete Größe a: $ \; \vec{a} $
Ein wesentlicher Unterschied zwischen Skalaren und Vektoren betrifft ihre Addierbarkeit. Skalare können einfach addiert werden. Es gilt dann: \begin{align} m_1 + m_2 & = m_{1+2} \\ 3 \; \text{kg} + 2 \; \text{kg} & = 5 \; \text{kg} \end{align} Für Vektoren gilt das nur, wenn die Größen parallel verlaufen. Siehe dazu die rechnerische Addition von Vektoren.
Vektoren kann man aber auch zeichnerisch zusammenfassen oder in mehrere einzelne Vektoren aufteilen. Dies geschieht meist aufgrund der zu lösenden Aufgabenstellung und hängt damit von den Bedingungen ab, die die Problemstellung liefert.
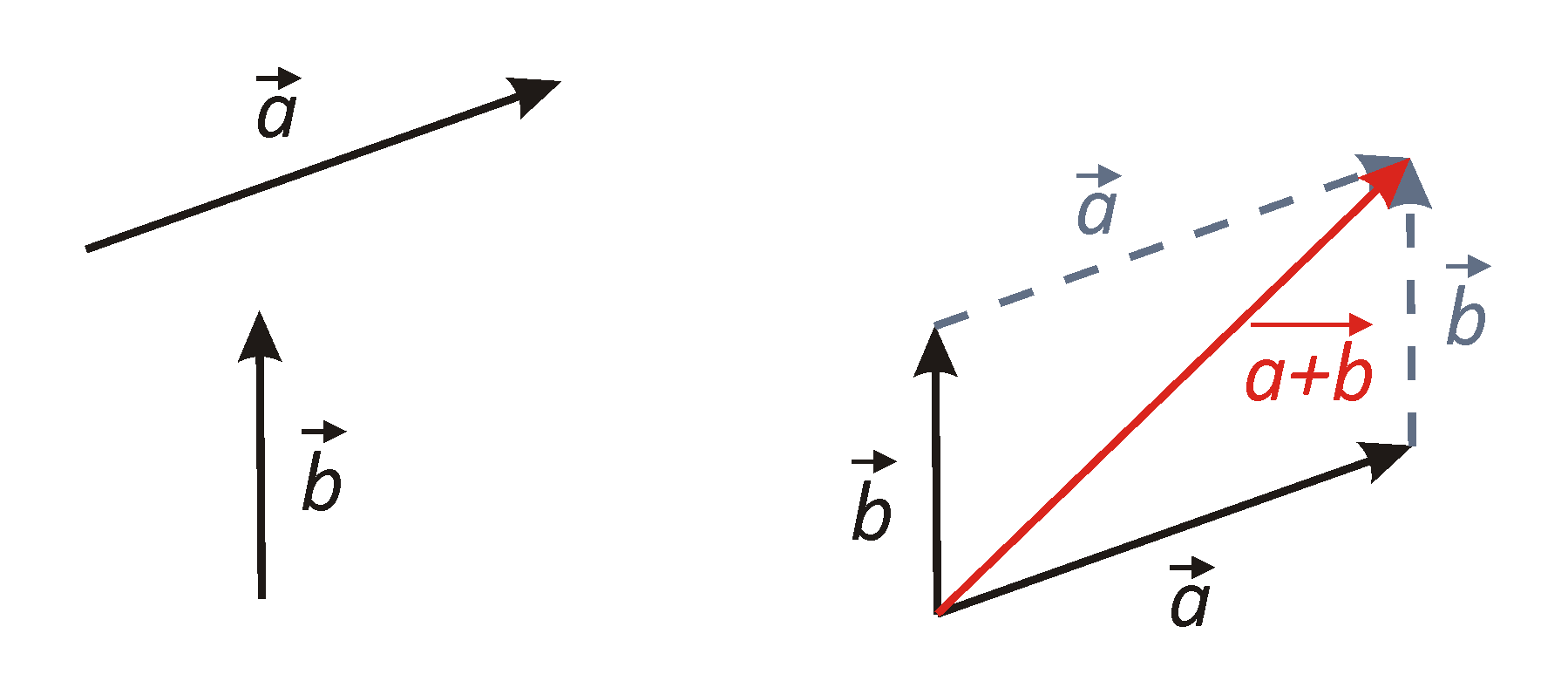
Es sind die beiden Vektoren $\vec {a}$ und $\vec{b}$ gegeben, die jeweils durch die entsprechenden Pfeile dargestellt sind. Die Pfeile dürfen parallel verschoben werden, denn die Richtung und die Länge der Pfeile verändern sich dadurch nicht.
Wenn beide Vektoren so verschoben werden, dass sie einen gemeinsamen Angriffspunkt haben, d.h. dass sie zusammen an einem Körper wirken, kann man beide Pfeile als zwei Seiten eines Parallelogramms auffassen, dessen Diagonale der Addition der beiden Vektoren entspricht. Die Reihenfolge der Addition ist gleichgültig. Es gilt: $$ \vec{a} + \vec{b} = \vec {b} + \vec{a} $$
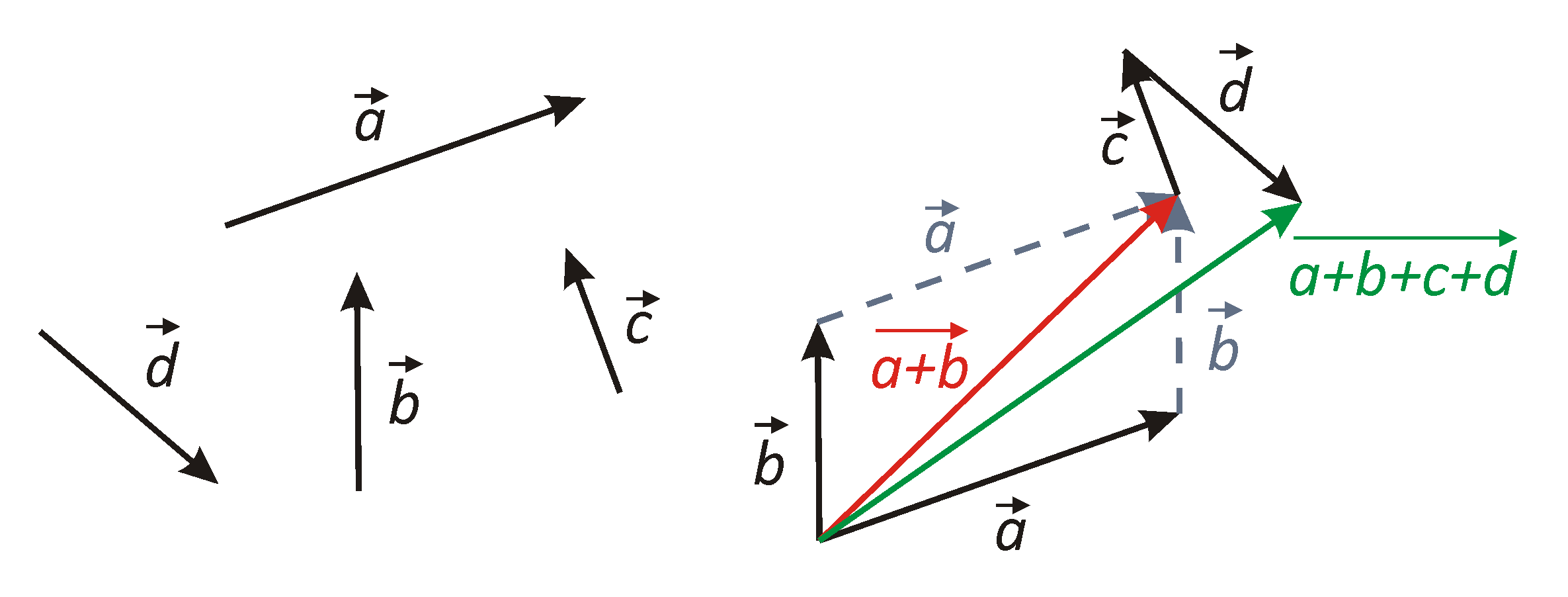Wenn mehr als zwei Vektoren zusammengefasst werden müssen, geht man entweder für jeden der Vektoren nacheinander
nach demselben Schema vor oder man hängt jeden neuen Vektor an das Ende des letzten Vektors. Die Verbindung des Startpunkts des ersten und
des Endes des letzten Vektors entspricht dann dem resultierendem Vektor.
Beispiel einer schiefen Ebene
Jeder Körper hat eine Masse $m$. Zusammen mit der Fallbeschleunigung $ \vec{g}$ erfährt der Körper eine Gewichtskraft $\vec{F_G}$.
Liegt dieser Körper auf einer schiefen Ebene, wird ein Teil der Gewichtskraft dazu genutzt, den Körper die Ebene hinab gleiten zu lassen, ein anderer Teil der Gewichtskraft wird genutzt, um den Körper auf den Boden der Ebene zu drücken.
Die Kraft, die den Körper die Ebene hinab gleiten lässt, nennt man Hangabtriebskraft $\vec{F_H}$.
Die Kraft, die den Körper auf den Boden drückt, nennt man in Anlehnung an die Mathematik Normalkraft $\vec{F_N}$.
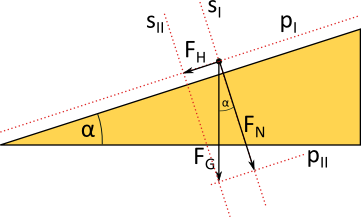
Die Gewichtskraft wirkt immer senkrecht nach unten, in Richtung Erdmittelpunkt. Wenn man eine schiefe Ebene, z.B. eine Bergstraße, vorliegen hat, werden aber die Kräfte benötigt, die parallel und senkrecht zum Untergrund verlaufen.
In der Skizze wird der Untergrund, bzw. die Linie, die den Untergrund repräsentiert, parallel soweit verschoben,
dass sie durch den Massepunkt des sich bewegenden Körpers verläuft. Das ist in der Skizze die Linie pI.
pI wird noch einmal soweit verschoben, dass sie durch den Endpunkt des Gewichtskraftvektors verläuft
(pII).
Durch den Massepunkt wird noch eine senkrecht zum Untergrund verlaufende Linie gezeichnet (sI), die ebenfalls
verschoben wird, bis sie durch den Endpunkt des Gewichtskraftvektors verläuft (sII).
Das so gewonnene Rechteck hat Kanten, die parallel und senkrecht zum Untergrund verlaufen. Wie man in der Skizze erkennen kann, bildet der Vektor der Gewichtskraft die Diagonale des Rechtecks, ist also die Resultierende der Vektoren, die die beiden Seiten des Rechtecks bilden. Die Länge der senkrecht zum Untergrund verlaufenden Seite gibt die Größe der Normalkraft an, die Länge der parallel verlaufenden Seite die Größe der Hangabtriebskraft.
Mit Hilfe des Steigungswinkels $\alpha$ kann man jetzt aus der Gewichtskraft die Normal- und die Hangabtriebskraft berechnen. Dazu bedient man sich der Formeln aus der Trigonometrie. Man erhält: \begin{align} \vec{F_H} & = \vec{F_G} \cdot \sin{\alpha} \\ \vec{F_N} & = \vec{F_G} \cdot \cos{\alpha} \end{align}
Mit den neuen Kräften $\vec{F_H}$ und $\vec{F_N}$ entfällt die alte Kraft $\vec{F_G}$. Sie darf in den weiteren Berechnungen und Überlegungen nicht mehr genutzt werden.
Wie bereits geschrieben, werden Vektoren oder vektorielle Größen mit einem Pfeil über dem Formelzeichen
angegeben. Bei den meisten Problemen und Aufgabenstellungen in der Physik werden jedoch die Komponenten der Vektoren in
bestimmten Richtungen benötigt. Bei dem Beispiel der schiefen Ebene wären das die benötigten Kräfte FH
und FN anstelle der gegebenen Kraft FG.
Wenn durch die Berechnung der entsprechenden Komponenten
des Vektors die Wirkungsrichtung festgelegt wurde, im Beispiel "schiefe Ebene" durch die Verwendung des Sinus und Cosinus,
können die Pfeile über den Formelzeichen weggelassen werden.
Bei der Gewichtskraft lässt man die Pfeile auch meist weg, da durch die Definition der Kraft die Wirkungsrichtung bereits
festgelegt ist.
Für die rechnerische Addition von vektoriellen Größen werden die Größen in ihre Anteile entlang der Achsen eines geeigneten Koordinatensystems zerlegt. Die so erhaltenen Größen können dann einfach betragsweise addiert werden. Die beiden resultierenden Größen werden dann wieder vektoriell addiert. Dies soll anhand eines Beispiels durchgerechnet werden.
Es ist eine Kraft $\vec{F_1}$ gegeben, die den Betrag 7 N hat und unter einem Winkel von 25° zur $x$-Achse wirkt, sowie eine Kraft $\vec{F_2}$ mit 4 N unter einem Winkel von -10°.
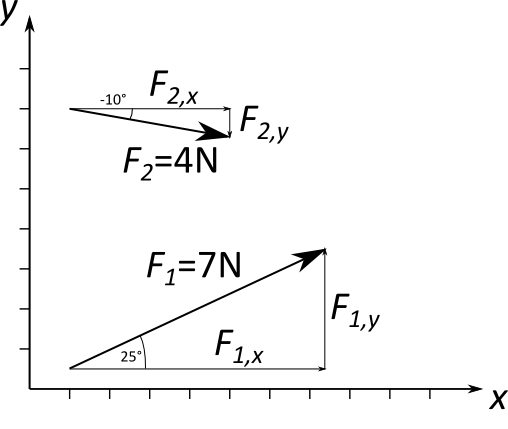
Mit Hilfe der Winkelbeziehungen des rechtwinkligen Dreiecks lassen sich die Anteile parallel zu den Achsen berechnen:
\begin{align}
F_{1,x} &= F_1 \cdot \cos{25^\circ} = 6,34 \; \text{N} \\
F_{2,x} &= F_2 \cdot \cos{(-10^\circ)} = 3,94 \; \text{N} \\
F_{1,y} &= F_1 \cdot \sin{25^\circ} = 2,96 \; \text{N} \\
F_{2,y} &= F_2 \cdot \sin{(-10^\circ)} = -0,69 \; \text{N}
\end{align}
$F_{1,x}$ und $F_{2,x}$ werden einfach addiert zu $F_{\text{Res},x}$,
ebenso $F_{1,y}$ und $F_{2,y}$ zu $F_{\text{Res},y}$:
\begin{align}
F_{\text{Res},x} &= 6,34 \; \text{N} + 3,94 \; \text{N} = 10,28 \;\text{N} \\
F_{\text{Res},y} &= 2,96 \; \text{N} - 0,69 \; \text{N} = \;\; 2,27 \; \text{N}
\end{align}
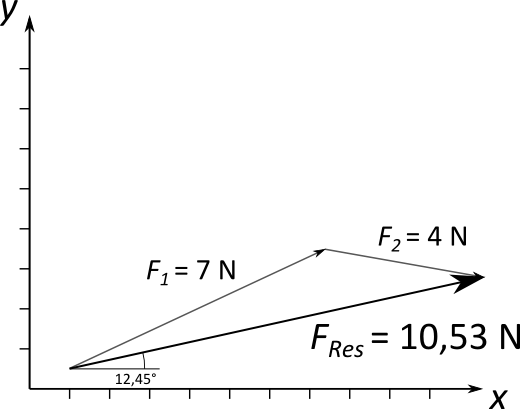
Mit dem Satz des Pythagoras wird die resultierende Kraft bestimmt: \begin{align} F_{\text{Res}}^2 &= F_{\text{Res},x}^2 + F_{\text{Res},y}^2 \\ F_{\text{Res}} &= 10,53 \; \text{N} \end{align} Durch die Tangensbeziehung wird der Winkel der resultierenden Kraft bezüglich der $x$-Achse bestimmt: \begin{align} \tan{\alpha} &= \frac{F_{\text{Res},y}}{F_{\text{Res},x}} \\ \alpha &= 12,45^\circ \end{align}
Zusätzlich ist in der Abbildung rechts die zeichnerische Addition gezeigt, die natürlich zum selben Ergebnis kommt.
Die Physik hat die Aufgabe, die wirkliche Welt zu erklären. Die physikalischen Größen, um die es dabei geht, hängen aber mit sehr vielen anderen physikalischen Größen zusammen. Sie hängen voneinander ab oder sie bedingen einander. Ein solchermaßen kompliziertes System kann von der Mathematik nicht mehr sinnvoll beschrieben werden. Beispielsweise ist es nicht in absehbarer Zeit möglich, ein Atom zu beschreiben und zu berechnen, das mehr als zwei Elektronen besitzt.
Aus diesem Grunde wurden und werden Modelle entwickelt, die wesentliche Aspekte des zu beschreibenden Systems beinhalten, aber andere Aspekte, die für diesen einen Zusammenhang nicht wichtig sind, beiseite lassen. Eines dieser vereinfachenden Modelle ist z.B. das Modell des Massepunktes, das schon weiter oben beschrieben wurde.
Modelle haben die Aufgabe, etwas berechenbar zu machen, wobei der Fehler durch Weglassen einzelner Aspekte möglichst gering bleiben soll. So gibt es in nahezu jedem Teilbereich der Physik ein sogenanntes Teilchenmodell, das etwas über die Wechselwirkung von Teilchen untereinander festlegt. Meist ist es so, dass die Teilchen bis auf mechanische Wechselwirkungen (Stöße) keinerlei Einfluss aufeinander haben.
Jedes Modell hat aber auch seine Grenzen, d.h. Fälle, in denen das Modell nicht mehr gültig ist. Beispielsweise wurde im Laufe der Jahre einige Modelle bezüglich des Atoms aufgestellt. Die Modelle wurden immer detaillierter und sind für immer größere Anwendungsbereiche gültig. Daraus folgt allerdings nicht, dass alte Modelle für die entsprechenden Bereiche nicht mehr gültig sind. Neuere Modelle haben meist auch die Eigenschaft, dass sie komplizierter sind. Für bestimmte Bereiche ist es aber nicht notwendig, überaus komplizierte Modelle zu verwenden, da auch durch einfachere Modelle alles wichtige berechnet werden kann.
Es ist z.B. ausreichend, das Rutherfordsche Atommodell zu bemühen, wenn es nur um die Tatsache geht, dass ein Atom einen positiv geladenen Kern mit einer bestimmten Größe besitzt. Für die quantenmechanische Unschärferelation, d.h. die Möglichkeit, dass das Elektron nicht mehr genau lokalisierbar ist, ist aber z.B. das Orbitalmodell notwendig.
© mondbrand MMXIX